Lesson Five: The Normal (Bell) Curve

The normal curve or the normal frequency distribution is a hypothetical distribution of scores that is widely used in statistical analysis. Since many psychological and physical measurements are normally distributed, the concept of the normal curve can be used with many scores. The characteristics of the normal curve make it useful in education and in the physical and social sciences.

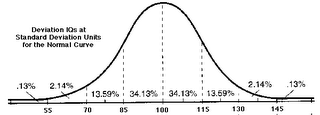
Deviation IQ Scores, sometimes called Wechsler IQ scores, are a standard score with a mean of 100 and a standard deviation of 15. We can thus see that the average IQ for the general population would be 100. If IQ is normally distributed, we would expect that two-thirds (68.26%) of the population would have deviation IQ's between 85 and 115. That is because 85 is one standard deviation below the mean and 115 is one standard deviation above the mean. We would expect that 99.72% of the distribution would lie within three standard deviations of the mean (that is IQs between 55 and 145).

The Stanford-Binet Scale of Intelligence IQ is also a standard score with a mean of 100 but with a standard deviation of 16. Thus a Wechsler IQ of 115 (one SD above the mean) would be equivalent to a Binet IQ of 116 (also one SD above the mean). A Wechsler IQ of 130 (two SDs above the mean) would be equivalent to a Binet IQ of 132. In some definitions of mental retardation, the cut off for an IQ score indicative of mental retardation is set at two standard deviations below the mean of the general population. This would be equivalent to a Wechsler IQ of 70 but a Stanford-Binet IQ of 68. We would also expect that 2.27% (.13% + 2.14% = 2.27%) of the population would have IQs this low.

Z-Scores
When a score is expressed in standard deviation units, it is referred to as a Z-score. A score that is one standard deviation above the mean has a Z-score of 1. A score that is one standard deviation below the mean has a Z-score of -1. A score that is at the mean would have a Z-score of 0. The normal curve with Z-scores along the abscissa looks exactly like the normal curve with standard deviation units along the abscissa.

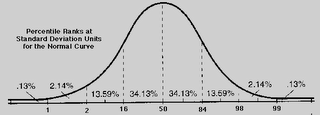
Percentile Ranks
Another useful derived score is the percentile rank. The percentile rank is the percentage or proportion of scores that score lower than a given score. If you received a percentile rank of 90 then 90% of the scores would be lower than your score and 10% of the scores would be higher. You could also say that your score is at the 90th percentile. The median for any set of scores (by definition) is at the 50th percentile. That is, 50% of the scores are lower than the median, and 50% of the scores are higher than the median. Ordinarily percentiles are reported as whole numbers so the highest percentile possible would be 99 and the lowest possible would be 1. A score that is one standard deviation below the mean would have a percentile rank of 16 (0.13 + 2.14 + 13.59 = 15.86). A score that is two standard deviations below the mean would have a percentile rank of 2 (0.13 + 2.14 = 2.27). A score that was three standard deviations below the mean would be at the 1st percentile and one that was three standard deviations above the mean would be at the 99th percentile. Some test designers have used the concept of extended percentile ranks to make finer divisions for scores at the upper half of the 99th percentile and at the lower half of the 1st percentile.

T-Scores
Another commonly used derived scores based on the normal curve, is the T-score. T-scores are derived scores with a mean of 50 and a standard deviation of 10. The average T-score for a group of scorers would be 50. We can see that a T-score of 60 would be equivalent to a Z-score of 1, and a Deviation IQ score of 115. Each of these scores would be one standard deviation above the mean and would be equal to or higher than 84.13% of the scores (50.00% + 34.13% = 84.13%)

http://www-stat.stanford.edu/~naras/jsm/NormalDensity/NormalDensity.html